Heapsort (Heapsort) refers to a sorting algorithm designed using the data structure of the heap. Stacking is a structure that approximates a complete binary tree, and at the same time satisfies the property of stacking: that is, the key value or index of a child node is always less than (or greater than) its parent node. Heap sort can be said to be a selection sort that uses the concept of heap to sort. There are two methods:
Large top heap: the value of each node is greater than or equal to the value of its child nodes, used in the heap sorting algorithm for ascending order;
small top heap: the value of each node is less than or equal to the value of its child nodes, in the heap Sorting algorithm is used to sort in descending order.
Algorithm steps (taking the construction of a large top heap as an example)
The steps to sort from small to large are as follows:
1. Construct a sequence of length n into a large top heap ;
2.
Swap the root node with the last node of the sequence, and the last node is the maximum value of the sequence;
3. Convert the remaining n - 1 node is again constructed into a large top heap;
4. Repeat steps
2 and 3 until the size of the heap is 1, and a completely ordered sequence is constructed.
The heap needs to meet two conditions:
1. It is a complete binary tree (Complete Binary Tree)
2.
Each node on the heap must satisfy that the value of the parent node is greater than or equal to the value of the child node or the value of the parent node is less than or equal to The value of the child node. parent >= children or parent
<= children
Algorithm diagram
We take int
tree[] = {6, 10, 3, 8, 5, 12, 7, 2, 9} as an example to illustrate the execution process of heap sort.
Step 1: Construct a large top heap from the original sequence (a large top heap is used for ascending order, and a small top heap is used for descending order).
1. First construct a complete binary tree through the sequence from top to bottom and left to right.
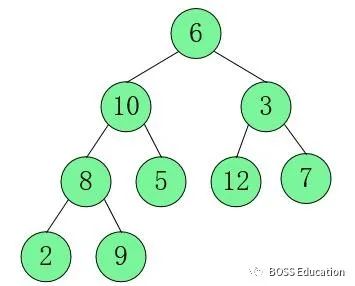
2. Adjust the parent node of the third layer and the child node of the fourth layer, where pink represents the node that exchanges. Make its parent node greater than two child nodes. That is, starting from the last
non-leaf node (8 - 1) / 2 = 3, that is, starting from 8 and adjusting from left to right and bottom to top.
In [8,2,9], 9 is the largest, swap 8 and
9.
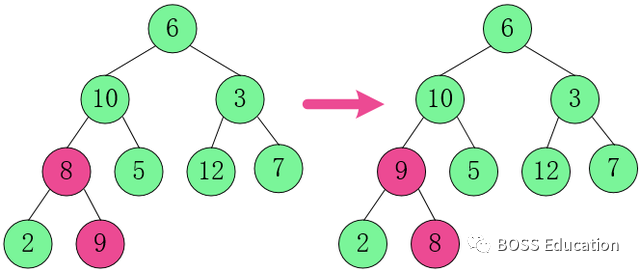
3. Adjust the parent node of the second layer and the child node of the third layer.
In [10,9,5], 10 is the largest, no swap.
In [3,12,7], 12 is the
largest, swap 3 and 12.
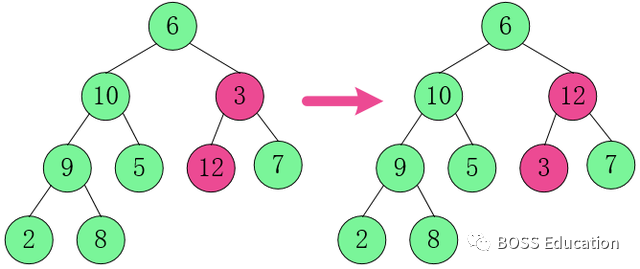
4. Adjust the parent node of the first layer and the child node of the second layer.
In [6, 10, 12]
, 12 is the largest, swap 6 and 12.
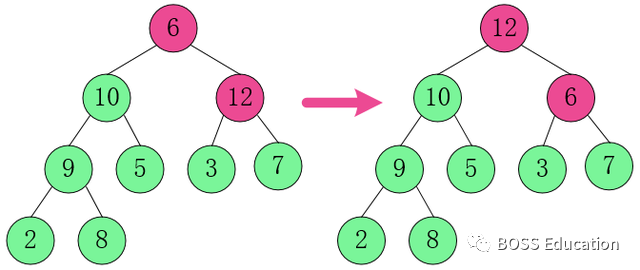
At this time, the above operation results in that [6,3,7] is not a large top heap, and continues to adjust.
In [6,3,7], 7 is the largest, swap 6
and 7.
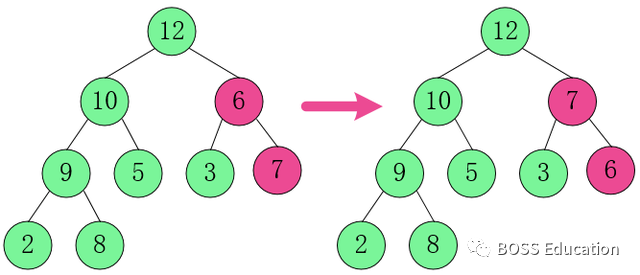
At this point, the construction of the big top heap is completed.
Step 2: Adjust the root node to the last position so that the last element is the largest. Then continue to adjust the heap for the remaining elements, the root node is adjusted to the last position, and the second largest element is obtained. Swap, refill, swap over and over again.
1.
Swap the root node element 12 with 8.
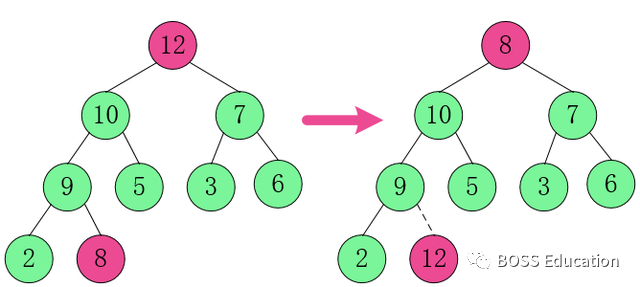
2. Restructure the structure so that it continues to satisfy the heap definition.
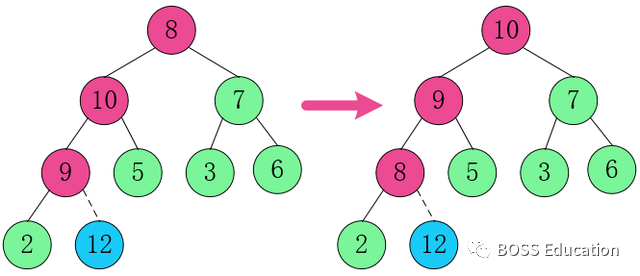
3. Swap the root node element 10 with 2.
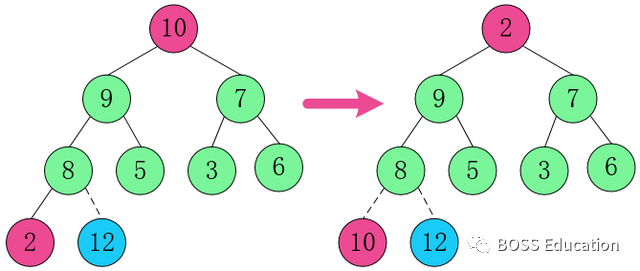
4. Restructure the structure so that it continues to satisfy the heap definition.
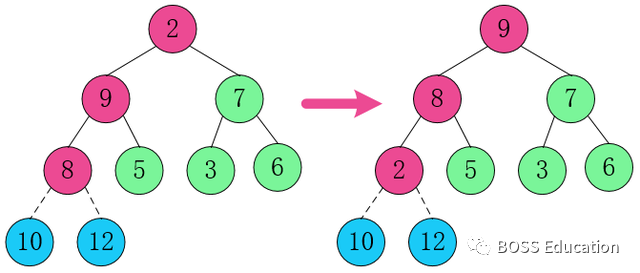
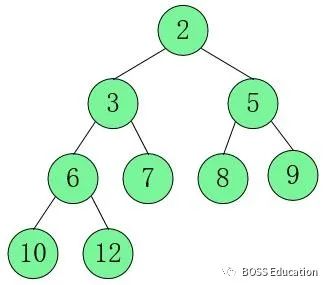
This has been swapped, refactored, swapped....
Finally, all elements have reached an ordered state.
Solution in Python
import randomSampleList=random.sample(range(1,1000),9)print("乱序排列为:")print(SampleList)def MaxHeapify(arr, dad, end):maxkey=dadlson = 2 * dad + 1 # left = 2*i + 1rson = 2 * dad + 2 # right = 2*i + 2if lson <= end and arr[dad] < arr[lson]:maxkey = lsonif rson <= end and arr[maxkey] < arr[rson]:maxkey = rsonif maxkey != dad:arr[dad], arr[maxkey] = arr[maxkey], arr[dad] # 交换MaxHeapify(arr, maxkey, end)def HeapSort(arr): # 建大堆。end = len(arr)-1for i in range(end, -1, -1):MaxHeapify(arr, i//2-1, end)# 一个个交换元素for i in range(end , 0, -1):arr[i], arr[0] = arr[0], arr[i] # 交换MaxHeapify(arr, 0, i-1)HeapSort(SampleList)n = len(SampleList)print("堆排序结果为:")print(SampleList)
Solution in C++
using namespace std;void MaxHeapify(int arr[], int start, int end);void HeapSort(int arr[], int len) ;int print(int A[],int n);int main(){int n=11;srand((unsigned int)time(0));int A[n];for(int i=0;i<n;i++){A[i]=rand()%1000;}cout<<"乱序排列为:"<<endl;print(A,n);HeapSort(A, n) ;cout<<"堆排序结果为:"<<endl;print(A,n);return 0;}int print(int A[],int n){for(int i=0;i<n;i++){cout<<A[i]<<" ";}cout<<endl;return 0;}void MaxHeapify(int arr[], int dad, int end)//此函数是判断大小并执行交换{int maxkey = dad;//获取父节点的下标,暂时认为父节点数值最大int lson = dad * 2 + 1;//左儿子节点,因为下标0开始所以需要+1int rson = dad * 2 + 2;//右儿子节点,因为下标0开始所以需要+2if (lson <= end and arr[lson] >arr[dad]) //先比较左儿子节点和父节点,选择最大的maxkey=lson;//若符合条件,指向左儿子节点if (rson <= end and arr[rson] >arr[maxkey]) //比较右儿子(如果有)节点和max(左儿子节点,父节点),选择最大的maxkey=rson;//若符合条件,指向右儿子节点if (maxkey!=dad){swap(arr[dad], arr[maxkey]);MaxHeapify(arr, maxkey, end); //儿子节点一旦与父节点交换值,儿子节点要继续与下级节点比较大小}}void HeapSort(int arr[], int len){//初始化,i从最后一个父节点开始调整,也就是从下到上进行调整,for (int i = len / 2 - 1; i >= 0; i--)//15个元素,最后一个父节点下标是6MaxHeapify(arr, i, len - 1);//数组下标是从0开始,所以end是len-1//执行到这一步就已经符合大根堆的结构了//使顶堆跟最后一个元素交换,这里i--达到弹出的效果,也就是i+1到len-1的范围都是已经排好序的,再重新调整使符合大根堆,直到排序完毕for (int j = len - 1;j >= 0; j--){swap(arr[0], arr[j]);MaxHeapify(arr, 0, j - 1);}}
▍Disclaimer : This article is organized from the Internet. If there is any infringement, please contact to delete it.
This official account publishes this article for the purpose of transmitting more information. If there is an error in the source labeling or infringement of your legal rights, please feel free to contact us for consultation, contact (QQ): 993225721, we will correct and delete it in time.
Love you to follow us-
