Python |
Focus on [MD] HVRP series solution algorithm
Tabu search algorithm
Summary
Tabu Search Algorithm + Split to Solve Heterogeneous Vehicle Path Planning Problem

Committed to building a high-quality code sharing platform in the field of transportation

Today, I will continue to share with you the source code of the [MD]HVRP series solving algorithm. Welcome: Like + Favorite + Follow . More high-quality content will be pushed in the future, in order to avoid missing 100 million, it is recommended to star .
Heterogeneous fixed fleet vehicle routing problem (HVRP) is an important variant of VRP. Compared with the original VRP, it further considers some characteristics of vehicles, such as loading capacity, mileage and so on. There are also some studies on certain characteristics of customers. The heterogeneity here refers to the difference in the loading capacity of the vehicle, which brings about the difference in transportation costs. In order to seek a better solution effect under multiple constraints, this article will reproduce the improved Split algorithm in the classic literature to realize the vehicle path planning problem that considers the vehicle loading characteristics under the condition of multiple (single) parking lots.
01
Precautions
Solving for HVRP or MDH VRP
Multiple vehicle types
The vehicle capacity is not less than the maximum demand of the demand node
(Multiple) Vehicle Base
The total number of vehicles in the parking lot meets the actual demand
02
Realize ideas
The Split method process of HVRP given by Christian Prins [2] is as follows:

In the above algorithm, the scale of candidate labels of the required nodes will be very large during the search process, which occupies memory and reduces the search efficiency. Therefore, the Pareto idea is used to inherit the non-dominated solution (lines 19 to 21). In order to further control the number of alternative labels, this article also implements the determination of whether to generate new alternative labels through the remaining capacity and remaining demand, so as to avoid the generation of infeasible labels in advance. Nevertheless, when there are many types of heterogeneous vehicles considered and the scale of demand points is large, the solution efficiency is still low (code structure, python characteristics, hardware environment). Therefore, this article further adds the parameter of the maximum number of labels to control the size of the alternative labels of each demand node, and achieves a relative balance between speed and quality by adjusting this parameter.
03
data structure
Continue to encapsulate algorithm parameters, encoding, decoding, objective functions, etc. in the form of classes. Specifically divided into the following four categories:
The basic data structure is defined as follows:
Sol class: contains information about the solution
| Attributes | describe |
|---|---|
| obj | Optimization target value |
| node_id_list | Demand node id ordered set collection |
| route_list | vehicle path collection |
| action_id | The operator id corresponding to the solution , used to disable the operator |
· Demand class: Contains information about demand nodes
| Attributes | describe |
|---|---|
| id | Physical node id, which must be unique. Numbering starts from 0 |
| x_coord | Physical node x coordinate |
| y_coord | Physical node y coordinate |
| demand | Physical Node Requirements |
Vehicle class: Contains information about vehicles
| Attributes | describe |
|---|---|
| depot_id | The id of the parking lot you belong to, which cannot be the same as the request id |
| capacity | vehicle loading rate |
| type | vehicle type |
| fixed_cost | fixed cost |
| variable_cost | Variable cost per mile |
| numbers | number of vehicles |
Model class : contains global parameters
| Attributes | describe |
|---|---|
| sol_list |
A collection of populations, the value type is Sol() |
| best_sol | Global optimal solution, the value type is Sol() |
| demand_dict | A collection of demand nodes (dictionary), the value type is Demand() |
| vehicle_dict | A collection of vehicles, the value type is Vehicle() |
| vehicle_type_list | Collection of vehicle types |
| demand_id_list | Requirement id collection |
| distance_matrix | distance matrix |
| number_of_demands | Quantity required |
| TL | Taboo length |
| tau_list | Taboo list |
| max_labels | Maximum number of alternative labels |
04
Part of the source code
parameter read

def readCSVFile(demand_file,depot_file,model):with open(demand_file,'r') as f:demand_reader=csv.DictReader(f)for row in demand_reader:demand = Demand()demand.id = int(row['id'])demand.x_coord = float(row['x_coord'])demand.y_coord = float(row['y_coord'])demand.demand = float(row['demand'])model.demand_dict[demand.id] = demandmodel.demand_id_list.append(demand.id)model.number_of_demands=len(model.demand_id_list)with open(depot_file, 'r') as f:depot_reader = csv.DictReader(f)for row in depot_reader:vehicle = Vehicle()vehicle.depot_id = row['depot_id']vehicle.x_coord = float(row['x_coord'])vehicle.y_coord = float(row['y_coord'])vehicle.type = row['vehicle_type']vehicle.capacity=float(row['vehicle_capacity'])vehicle.numbers=float(row['number_of_vehicle'])vehicle.fixed_cost=float(row['fixed_cost'])vehicle.variable_cost=float(row['variable_cost'])model.vehicle_dict[vehicle.type] = vehiclemodel.vehicle_type_list.append(vehicle.type)

def calDistanceMatrix(model):for i in range(len(model.demand_id_list)):from_node_id = model.demand_id_list[i]for j in range(i + 1, len(model.demand_id_list)):to_node_id = model.demand_id_list[j]dist = math.sqrt((model.demand_dict[from_node_id].x_coord - model.demand_dict[to_node_id].x_coord) ** 2+ (model.demand_dict[from_node_id].y_coord - model.demand_dict[to_node_id].y_coord) ** 2)model.distance_matrix[from_node_id, to_node_id] = int(dist)model.distance_matrix[to_node_id, from_node_id] = int(dist)for _, vehicle in model.vehicle_dict.items():dist = math.sqrt((model.demand_dict[from_node_id].x_coord - vehicle.x_coord) ** 2+ (model.demand_dict[from_node_id].y_coord - vehicle.y_coord) ** 2)model.distance_matrix[from_node_id, vehicle.type] = int(dist)model.distance_matrix[vehicle.type, from_node_id] = int(dist)

def calTravelCost(route_list,model):obj=0for route in route_list:vehicle=model.vehicle_dict[route[0]]distance=0fixed_cost=vehicle.fixed_costvariable_cost=vehicle.variable_costfor i in range(len(route) - 1):from_node = route[i]to_node = route[i + 1]distance += model.distance_matrix[from_node, to_node]obj += fixed_cost + distance * variable_costreturn obj
Objective function calculation

def calObj(node_id_list,model):vehicle_routes = splitRoutes(node_id_list, model)if vehicle_routes:return calTravelCost(vehicle_routes,model),vehicle_routeselse:return 10**9,None
initial solution

def generateInitialSol(node_id_list):node_id_list_=copy.deepcopy(node_id_list)random.seed(0)random.shuffle(node_id_list_)return node_id_list_
Neighborhood operator

def createActions(n):action_list=[]nswap=n//2# 第一种算子(Swap):前半段与后半段对应位置一对一交换for i in range(nswap):action_list.append([1,i,i+nswap])# 第二中算子(DSwap):前半段与后半段对应位置二对二交换for i in range(0,nswap,2):action_list.append([2,i,i+nswap])# 第三种算子(Reverse):指定长度的序列反序for i in range(0,n,4):action_list.append([3,i,i+3])return action_list
Extract path

def extractRoutes(V,node_id_list,model):route_list = []min_obj=float('inf')pred_label_id=Nonev_type=None# search the min cost label of last node of the node_id_listfor label in V[model.number_of_demands-1]:if label[3]<=min_obj:min_obj=label[3]pred_label_id=label[1]v_type=label[2]# generate routes by pred_label_idroute=[node_id_list[-1]]indexs=list(range(0,model.number_of_demands))[::-1]start=1while pred_label_id!=1:for i in indexs[start:]:stop=Falsefor label in V[i]:if label[0]==pred_label_id:stop=Truepred_label_id=label[1]start=iv_type_=label[2]breakif not stop:route.insert(0,node_id_list[i])else:route.insert(0,v_type)route.append(v_type)route_list.append(route)route=[node_id_list[i]]v_type=v_type_route.insert(0,v_type)route.append(v_type)route_list.append(route)return route_list
05
code structure
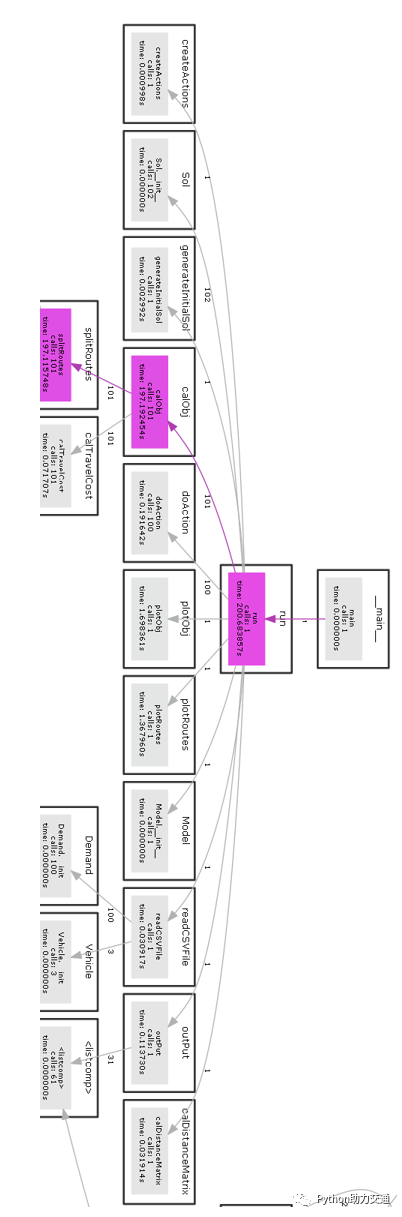
06
Results display
Solomon open source data is used to test the algorithm here. The data file structure is shown in the figure below, with a total of 100 demand points, 3 parking lots, and 3 types of vehicles. The data is stored in a .csv file.
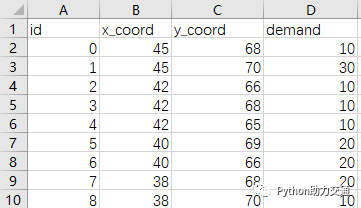
The content of the demand.csv file is as shown in the figure below, in which the first row is the title bar, and the node id is incremented from 0.


The content of the depot.csv file is as shown in the figure below, in which the first row is the title bar, in order: yard id, yard plane x coordinate, yard plane y coordinate, vehicle type, vehicle load, vehicle quantity, fixed cost, and transportation cost per mile.

The solution result is as follows:
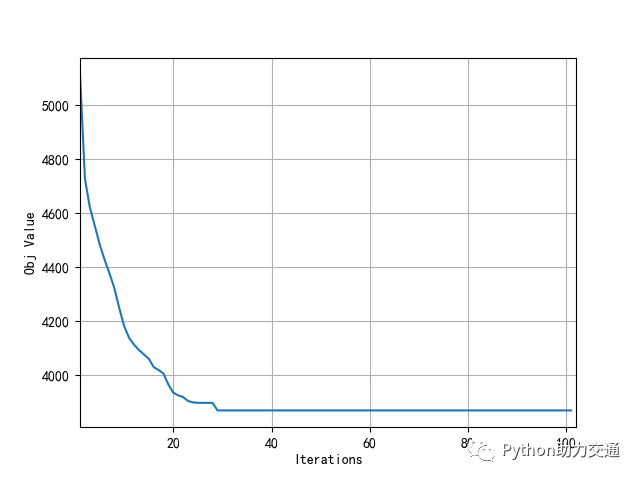
Algorithm Convergence Graph
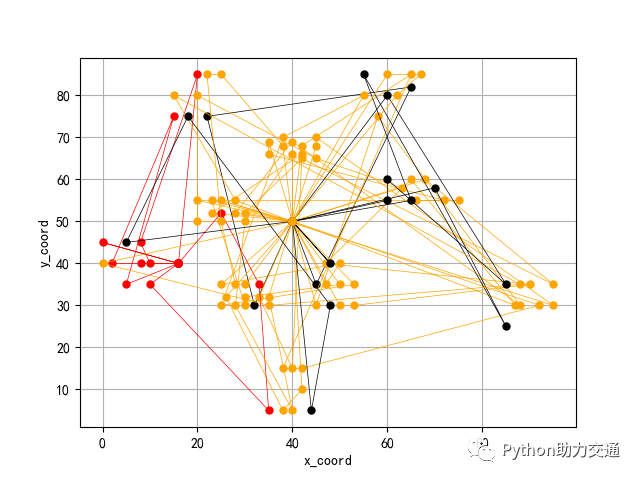
Optimization Roadmap
07
Source code acquisition
①Share to Moments for more than 1 hour
② Reply to 'TS_HVRP' in the background by sharing the screenshot to get the download link (the link is valid for 30 days)
08
reference
[1]. Wang Dingwei. Intelligent Optimization Method [M]. Higher Education Press, 2007.
[2] Prins C , Lacomme P , Prodhon C . Order-first split-second methods for vehicle routing problems: A review[J]. Transportation Research Part C, 2014, 40(mar.):179-200.
Scan the code to follow us
Welcome to like + favorite + follow

Editor | Guo Xiaoan
proofread | cover
point to share

Favorites

Like

click to see