Python: Jaccard similarity and distance

👇 Lianxh Club Tweet Navigation | www.lianxh.cn

🍎 Stata: Stata Basics | Stata Drawing | Stata Programs | Stata New Commands
📘 Papers: data processing | result output | paper writing | data sharing
💹 Metrics: Regression Analysis | Intersection-Conditioning | IV-GMM | Time Series | Panel Data | Spatial Metrics | Probit-Logit | Quantile Regression
⛳ Topic: SFA-DEA | Survival Analysis | Crawler | Machine Learning | Text Analysis
🔃 Causality: DID | RDD | Causal Inference | Synthetic Control Method | PSM-Matching
🔨 Tools: Tools | Markdown | Python-R-Stata
🎧 Course: Open Class-Live | Metrology Topics | About Lianxianghui

Lianxianghui 2022 Special Topic on Spatial Measurement

Author : Liang Shuzhen (Huaqiao University)
Email : [email protected]

Editor's note : This article is mainly compiled from "Jaccard similarity and Jaccard distance in Python", thank you!

Reminder: The link in the text does not take effect in WeChat. Please click "Read the original text" at the bottom . Or directly long press/scan the following QR code to go directly to the original text:

Table of contents

1 Introduction
2. Definition of Jaccard similarity
3. Calculation of Jaccard similarity
4. Definition of Jaccard distance
5. Calculation of Jaccard distance
6. Similarity and distance of asymmetric binary variables
7. Python calculate Jaccard similarity
8. Python calculate Jaccard distance
9. Python computes asymmetric binary variables
10. Python calculates the similarity of Chinese Jaccard
11. Related Tweets

1 Introduction

Jaccard similarity is widely used in the calculation of similarity between data, such as set similarity, text similarity, etc. The Python instance in this article needs to use three modules, scipy, and . The specific installation commands are as follows:sklearnnumpy

pip install scipy
pip install sklearn
pip install numpy

2. Definition of Jaccard similarity

Jaccard similarity (also known as Jaccard similarity coefficient, or Jaccard index) is a statistic used to calculate the similarity between two sets, and can be extended to the calculation of text similarity. In Python, Jaccard similarity is mainly used to calculate the similarity of two sets or asymmetric binary variables. Mathematically, Jaccard similarity can be expressed as the ratio of intersection and union. Take set A and set B as an example:

The formula for calculating the Jaccard similarity is:

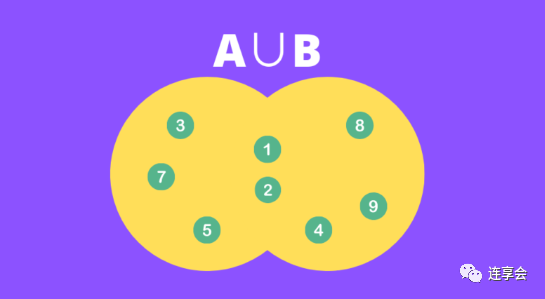
The numerator part of the formula is the intersection of the two sets, as shown in the yellow part of the following figure:

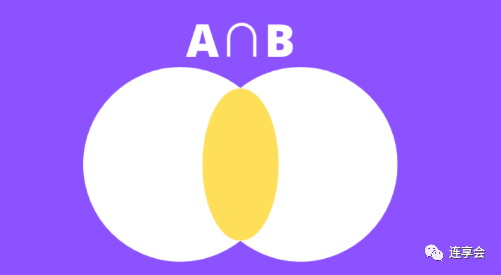
The denominator part of the formula is the union of the two sets, as shown in the yellow part of the following figure:

Mathematically, the Jaccard similarity can be understood as the ratio of the number of intersection elements to the number of union elements in the above figure, specifically:

If the two sets are equal, such as and , then the Jaccard similarity is 1;
If the two set elements are completely different, such as and , then the Jaccard similarity is 0;
The Jaccard similarity is between 0 and 1 if the two sets have some of the same elements, eg and .

3. Calculation of Jaccard similarity

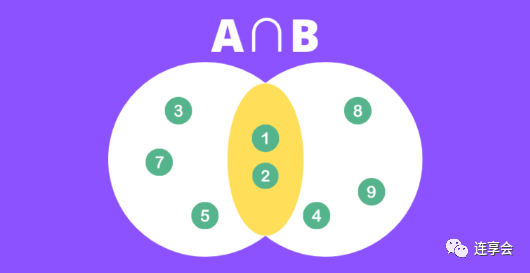
Consider the following two sets: and , which can be represented in the graph as:

Step 1: Find the intersection of the two sets. In this example, .

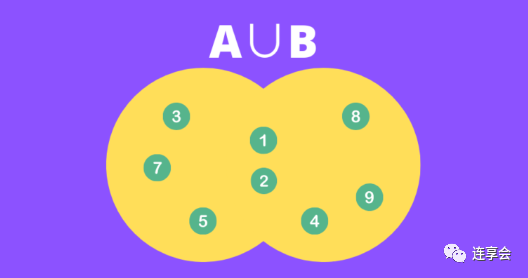
Step 2 : Find the union of the two sets. In this example, .

Step 3 : Calculate the ratio.

4. Definition of Jaccard distance

Unlike Jaccard similarity, Jaccard distance measures how dissimilar two sets are. Mathematically, it can be expressed as the ratio of the complement to the union of the intersection. Also take set A and set B as an example:

The formula for the Jaccard distance is:

The numerator of the Jaccard distance can also be expressed as:

It can be more intuitively understood as the difference between the two sets, as shown in the yellow part of the following figure:

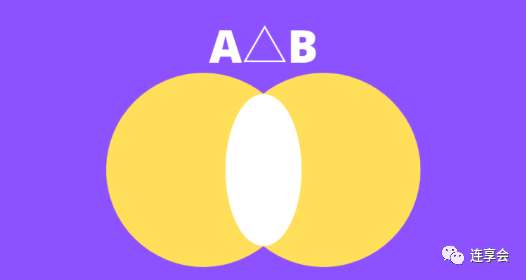
The denominator of the Jaccard distance is the same as the Jaccard similarity, which is the union of the two sets.

Mathematically, the Jaccard distance can be understood as the ratio of the number of set difference elements to the number of union elements. specifically:

If the two sets are equal, such as and , then the Jaccard distance is 0;
If two set elements are completely different, such as and , then the Jaccard distance is 1;
If two sets have partially identical elements, such as and , then the Jaccard distance is between 0 and 1.

5. Calculation of Jaccard distance

Consider the following two sets: and , which can be represented in the graph as:

Step 1: Find the complement of the intersection of the two sets.

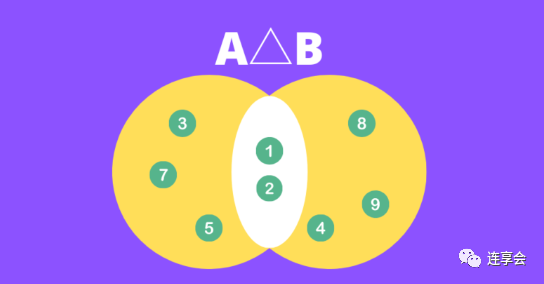
Step 2 : Find the union of the two sets. In this example, .

Step 3 : Calculate the ratio.

6. Similarity and distance of asymmetric binary variables

This section will discuss the specific application of Jaccard similarity and Jaccard distance to asymmetric binary variables.

A binary variable , as the name suggests, has only two categories or states. When the value is 0, it means that the state does not appear; when the value is 1, it means that the state appears. For example, smoker represents a patient object, 1 means the patient smokes, and 0 means the patient does not smoke. If it is a symmetric binary variable , its two attributes have the same weight, ie different states are coded with 0 or 1 and have no preference (eg 0 and 1 are coded for the gender variable).

The two outcomes of asymmetric binary variables are of different importance. For example, the results of nucleic acid testing are divided into positive and negative, positive results are coded with 1 (the probability is lower, the result is more important), and negative results are coded with 0. Given two asymmetric binary variable objects, the case where both objects take 1 is more important and meaningful than the case where both objects take 0.

Assuming that there are two n-dimensional vectors A and B, the calculation formula of Jaccard similarity is:

The formula for calculating the Jaccard distance is:

in,

Represents the number of two vectors whose corresponding components are both 1;
Represents the number of corresponding components of the two vectors are 0 and 1;
Represents the number of corresponding components of the two vectors are 1 and 0;
Represents the number of two vectors whose corresponding components are both 0.

and .

We understand it through a simple case. For example, a store sells 6 kinds of commodities (apples, tomatoes, eggs, milk, coffee, sugar), and there are two customer purchase records:

Customer A buys: apples, milk and coffee
Customer B buys: eggs, milk and coffee

From the above information, the following matrix can be constructed:

	Apple	Tomato	Eggs	Milk	Coffee	Sugar
A	1	0	0	1	1	1
B	0	0	1	1	1	0

For each commodity, the purchase decision is a binary variable, with 1 for buying and 0 for not buying. Next, we calculate Jaccard similarity and Jaccard distance in two steps:

Step 1: Find the M value

	quantity	illustrate
(M_{11})	2	Both A and B bought milk and coffee
(M_{01})	1	A did not buy eggs, B bought eggs
(M_{10})	2	A bought apples and sugar, but B didn't
(M_{00})	1	Neither A nor B bought tomatoes

And , it is the same as the number of products, and it is verified.

Step 2 : Substitute into the formula, then

Jaccard similarity:

Jaccard distance:

7. Python calculate Jaccard similarity

Define two collections in Python:

A = {1, 2, 3, 5, 7}
B = {1, 2, 4, 8, 9}

The construction function calculates the Jaccard similarity, passing the set A and set B as parameters to the function:

def jaccard_similarity(A, B):
    # 求集合 A 和集合 B 的交集
    nominator = A.intersection(B)
    # 求集合 A 和集合 B 的并集
    denominator = A.union(B)
    # 计算比率
    similarity = len(nominator)/len(denominator)
    return similarity
similarity = jaccard_similarity(A, B)
print(similarity)

The result is 0.25, which is the same as the manually calculated result.

8. Python calculate Jaccard distance

Calculate the Jaccard distance using the same data:

def jaccard_distance(A, B):
    #Find symmetric difference of two sets
    nominator = A.symmetric_difference(B)
    #Find union of two sets
    denominator = A.union(B)
    #Take the ratio of sizes
    distance = len(nominator)/len(denominator)
    return distance
distance = jaccard_distance(A, B)
print(distance)

The result is 0.75, the same as the manually calculated result.

9. Python computes asymmetric binary variables

# 导入模块
import numpy as np
from scipy.spatial.distance import jaccard
from sklearn.metrics import jaccard_score

Create two vectors from the matrix:

	Apple	Tomato	Eggs	Milk	Coffee	Sugar
A	1	0	0	1	1	1
B	0	0	1	1	1	0

A = np.array([1,0,0,1,1,1])
B = np.array([0,0,1,1,1,0])
similarity = jaccard_score(A, B)
distance = jaccard(A, B)
print(f'Jaccard similarity is equal to: {similarity}')
print(f'Jaccard distance is equal to: {distance}')

The result obtained is:

Jaccard similarity is equal to: 0.4
Jaccard distance is equal to: 0.6

10. Python calculates the similarity of Chinese Jaccard

import pandas as pd
import jieba
import re

# 调用数据
data = pd.read_excel("https://file.lianxh.cn/data/m/mda.xlsx")
stopwords = pd.read_csv("https://file.lianxh.cn/data/c/cn_stopwords.txt", names=["stopwords"])

# 定义分词函数def cut_words(text):
def cut_words(text):
    words_list = []
    text = re.sub("[\W\d]", "", text) # 替换符号和数字
    words = jieba.lcut(text)
    for word in words:
        if word not in list(stopwords["stopwords"]):
            words_list.append(word)
    return" ".join(words_list)

# 对文本分词
data["BusDA"] = data["BusDA"].apply(cut_words)
data

# 定义 jaccard 相似度函数
def jaccard_similarity(list1, list2):
    s1 = set(list1)
    s2 = set(list2)
    return float(len(s1.intersection(s2)) / len(s1.union(s2)))

jaccard_similarity(data["BusDA"][1], data["BusDA"][1])

11. Related Tweets

Note: The Stata command that produces the following list of tweets is:
lianxh python, m
install the latest version lianxhcommand :
ssc install lianxh, replace

Topics: Topics Courses

Stata+Python: Crawling stocks to record highs in a straight flush

Topic: Data Sharing

Python+Stata: How to Get China Meteorological Historical Data

Topic: Text Analysis - Crawler

Python: Calculate cosine similarity for management discussion and analysis
Stata+Python: Crawling the list of stocks with record highs
Python: Crawling Oriental Fortune Stocks Comments for Sentiment Analysis
VaR Value at Risk: Stata and Python Implementation
Support Vector Machines: Stata and Python Implementation
Python Crawler: Analysis of Research Hotspots and Themes in Economic Research

Topic: Python-R-Matlab

Stata+Python: New Ideas for Importing Large Excel Documents - Taking Guotai An as an Example
Stata-Python Interaction-10: Configuration and Application of PyStata New Features of Stata17
Python：多进程、多线程及其爬虫应用
Python：爬取动态网站
Python爬取静态网站：以历史天气为例
Python：绘制动态地图-pyecharts
Python爬虫1：小白系列之requests和json
Python爬虫2：小白系列之requests和lxml
Python爬虫：爬取华尔街日报的全部历史文章并翻译
Python爬虫：从SEC-EDGAR爬取股东治理数据-Shareholder-Activism
Python：爬取巨潮网公告
Python：爬取上市公司公告-Wind-CSMAR
Python: 6 小时爬完上交所和深交所的年报问询函
Python: 使用正则表达式从文本中定位并提取想要的内容

课程推荐：因果推断实用计量方法
主讲老师：邱嘉平教授
🍓 课程主页：https://gitee.com/lianxh/YGqjp

New！ Stata 搜索神器：lianxh 和 songbl GIF 动图介绍
搜：推文、数据分享、期刊论文、重现代码 ……
👉 安装：
. ssc install lianxh
. ssc install songbl
👉 使用：
. lianxh DID 倍分法
. songbl all

🍏 关于我们

连享会 ( www.lianxh.cn，推文列表) 由中山大学连玉君老师团队创办，定期分享实证分析经验。
直通车： 👉【百度一下：连享会】即可直达连享会主页。亦可进一步添加「知乎」,「b 站」,「面板数据」,「公开课」等关键词细化搜索。